A Matemática na sua xícara de café, pois bem, você sabia que conceitos matemáticos ajudam a entender o que ocorre quando você se mistura o açúcar ao café? O café da manhã dos matemáticos pode ser bem mais complexo do que para os demais habitantes do planeta. Quando os matemáticos enchem suas xícaras de café e pegam o açúcar, eles reconhecem a mágica que ocorre durante o tempo em que a colher gira para misturar aquelas substâncias. Mas que beleza oculta os matemáticos veem na transformação do líquido amargo em doce?
Em primeiro lugar, eles sabem o quanto o caos é importante nesse processo e balançam a colher de forma desordenada. Se a mexessem em círculos, com movimentos periódicos, o açúcar se acumularia nas beiradas da xícara, onde o líquido se movimenta mais devagar. “O caos é usado em muitas aplicações práticas para fazer misturas de maneira a homogeneizar as substâncias”, conta o professor aposentado Hildebrando Rodrigues, do Instituto de Ciências Matemáticas e de Computação (ICMC) da USP, em São Carlos.
Ele explica que, ao promover o caos com a colher, possibilitamos que as partículas de açúcar se afastem rapidamente umas das outras e se mesclem com o líquido. “Essa é uma característica muito importante do caos: fazer o que está próximo se distanciar rapidamente”, revela o professor. Para analisar o fenômeno matematicamente, precisamos transformar o café e o açúcar em coordenadas: imagine, então, que o café se torna um “x” e o açúcar um “y”. A compreensão dessa mistura de “x” e “y” só ocorre se levarmos em conta os movimentos com eles ao longo do tempo em que a colher promove o deslocamento dessas duas coordenadas.

O professor Rodrigues é um dos principais expoentes da área de equações diferenciais no Brasil. Ele contribuiu para o desenvolvimento e a consolidação desse campo de pesquisa no País.
Bem-vindo ao sistema dinâmico da xícara de café! Observe o açúcar se misturando. Trata-se de um fenômeno em que há uma variação e você já consegue imaginar que esse microssistema funciona de forma similar a muitos outros. Olhe agora para o céu e veja os corpos celestes descrevendo suas órbitas: eles também se movem ao longo do tempo. E tudo que apresenta variação pode ser traduzido matematicamente por uma equação diferencial.
“No embrião do estudo das equações diferenciais está a obra de Galileu Galilei ao pesquisar o movimento dos astros”, conta Plácido Táboas, outro professor aposentado do ICMC. Ele lembra que no tempo de Galileu ainda não existia o termo “equações diferenciais” nem “cálculo diferencial”, mas faz uma ressalva: “Você tem que olhar a obra do homem no seu tempo. E no tempo dele, Galileu foi genial”.
Precursor da física experimental e teórica, Galileu deu os primeiros passos rumo à compreensão dos sistemas dinâmicos ao pesquisar a trajetória dos planetas. De lá para cá, muita coisa mudou. Hoje, a maioria dos modelos matemáticos utilizados na física, na engenharia, na química, na biologia e nos mercados financeiros envolve equações diferenciais. Elas são a base da dinâmica de Isaac Newton e estão presentes nas equações de Albert Einstein que descrevem a força da gravidade.
As equações diferenciais permeiam nosso cotidiano e são aplicadas a problemas tão diversos e fascinantes que vão muito além da mistura de café e açúcar. Foram elas que ajudaram a descobrir por que algumas pontes caem, quais obras de arte são falsas, a diagnosticar doenças, a acompanhar a evolução de um tumor cancerígeno e o crescimento de populações.
Ao vislumbrar essas diferentes aplicações, você verá que não é preciso fazer contas nem resolver equações para entender que a matemática está presente em tudo. É claro que talvez poucos sejamos capazes de resolver equações diferenciais, mas com certeza todos podemos reconhecer sua importância ao compreender para que elas servem. Basta pensar em tudo o que existe na vida que varia com o tempo e você começará a enxergar equações diferenciais por toda parte.
Uma ponte que cai
A terceira maior ponte pênsil do mundo foi inaugurada em 1940 no estreito de Tacoma, em Washington, nos Estados Unidos. Logo virou atração: as pessoas vinham de centenas de quilômetros em seus carros apreciar a curiosa emoção de dirigir sobre uma ponte que oscilava e havia ganhado o apelido de “galopante”. Poucos imaginavam que, quatro meses depois, o galope seria incontrolável a ponto de fazer a ponte de Tacoma Narrows despencar.
No livro Equações diferenciais e suas aplicações, o matemático Martin Braun conta os detalhes da tragédia, relatando que a única vida perdida na catástrofe foi a do cachorro de estimação de um repórter pouco cauteloso. Ele precisou abandonar o carro às pressas antes que a ponte desabasse e esqueceu o animal. “A partir de aproximadamente sete horas da manhã, de 7 de novembro de 1940, a ponte começou a ondular persistentemente por três horas”, relata Braun. A ponte só se despedaçou por completo às 11h10 daquela manhã. Mas o que essa queda tem a ver com as equações diferenciais?
“Imagine uma criança no balanço. Digamos que ela é pesada e, aos poucos, você a empurra e a faz se movimentar. Se você empurra na hora certa, ela vai embalando. Isso é ressonância: a força que você está fazendo ao empurrá-la entra em sintonia com a oscilação que já estava acontecendo e, então, ela vai oscilando com uma amplitude cada vez maior. E você faz isso com pouco esforço”, revela o professor Táboas. Foi esse fenômeno da ressonância que ocorreu na ponte de Tacoma: a frequência de vibração natural da ponte foi amplificada pelo vento que havia no local.
“Quanto perigo esse tipo de movimento apresenta depende de como a frequência natural da estrutura (lembremos que as pontes são feitas de aço, um material altamente elástico) está próxima da frequência da forma que empurra. Se as duas frequências são as mesmas, ocorre ressonância, e as oscilações se tornarão destruidoras se o sistema não tiver uma suficiente quantidade de amortecimento”, escreve Braun. O gráfico a seguir ilustra o fenômeno da ressonância, que também pode ser traduzido por meio de uma equação diferencial.
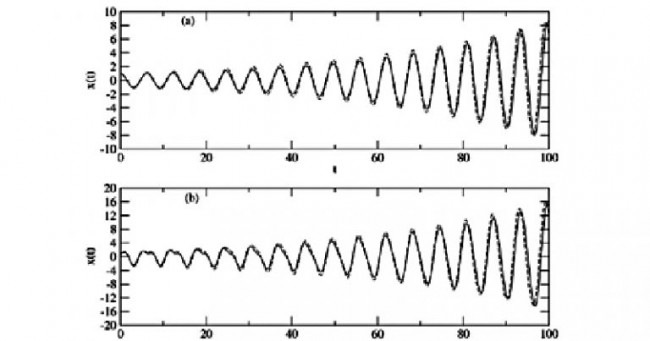
No livro, Braun relata que o mesmo fenômeno foi responsável pela queda da ponte suspensa de Broughton, perto de Manchester, na Inglaterra, em 1831. Mas em vez do vento, o responsável pelo desastre foram os soldados. Ao marcharem de forma cadenciada sobre a ponte, eles produziram uma força periódica de amplitude bastante grande, tal como o vento fez com a ponte de Tacoma. A frequência da força dos soldados foi igual à frequência natural da ponte e as oscilações foram aumentando até que a ponte ruiu: “É por essa razão que se ordena aos soldados para quebrarem a cadência quando atravessam uma ponte”.
Quando fala o coração
A marcha dos soldados pode ser comparada ao ritmo do nosso coração. Mas se a cadência desse órgão vital for quebrada, teremos um sério problema: arritmias cardíacas. Em um artigo publicado pelo professor Hildebrando Rodrigues, em parceria com a professora Isabel Laboriau, da Universidade do Porto, em Portugal, ele usou as equações diferenciais para modelar a atividade elétrica em sistemas biológicos.
A grande contribuição da matemática para essa área é atuar na busca pela sincronização desses sistemas quando eles entram em caos. Porque se o caos é muito bem-vindo na xícara de café, ele é um desastre quando interfere em batimentos cardíacos, impulsos nervosos, fibras musculares e células pancreáticas.
“As células do coração têm que pulsar de forma sincronizada tal como as linhas de transmissão de energia. Se acontecer uma falha em uma linha por causa de um raio, por exemplo, todo o sistema pode cair. E o caos pode se propagar caso aquela linha com problema não seja desligada”, explica Rodrigues. “No Brasil, temos mais de 600 hidrelétricas e cada uma tem seu próprio modelo matemático. Elas são interligadas pelas linhas de transmissão e todas têm que trabalhar sincronizadamente”, acrescenta o professor.
Rodrigues ressalta ainda que, a partir de um trabalho de colaboração com pesquisadores da área de engenharia elétrica, foram aprimorados os modelos empregados nessa área no Brasil. “Posso afirmar que os resultados mais bem-sucedidos para encontrar a estabilidade nesses sistemas de potência são do nosso grupo de pesquisa e podem ser utilizados em outras áreas do conhecimento.” O professor é um dos principais expoentes da área de equações diferenciais no Brasil. Ele contribuiu para o desenvolvimento e a consolidação desse campo de pesquisa no País.
Em 2013, ao completar 70 anos, ele foi homenageado durante o Summer Meeting on Differential Equations, um dos mais importantes eventos do mundo na área de equações diferenciais. Realizado anualmente pelo ICMC desde 1996, o evento é promovido pelo grupo de Sistemas Dinâmicos Não Lineares do ICMC e conta com o apoio das principais agências de fomento à pesquisa do País.
“Em muitos casos, estudamos as equações diferenciais como objetos matemáticos. A razão é que nós nunca sabemos quando vamos precisar delas. Mas é necessário ter essa caixa de ferramentas, que é uma completa compreensão da teoria, exatamente por não sabermos quando vamos necessitar dela em uma aplicação”, destaca o professor John Mallet-Paret, da Brown University, nos Estados Unidos.
Enquanto toma um café em um dos intervalos da última edição do Summer Meeting on Differential Equations, realizado de 6 a 8 de fevereiro no ICMC, ele dá inúmeros exemplos das aplicações das equações diferenciais: na física, são elas que ajudam a compreender o comportamentos dos fluidos e possibilitam, por exemplo, construir um avião mais eficiente ou fazer previsões do tempo; na biologia, é essa ferramenta que se usa para entender como as bactérias e os vírus se propagam, assim como para verificar se novas terapias são, de fato, melhores do que as antes empregadas.
Por isso, são muitos os desafios que instigam os pesquisadores dessa área. “Um dos campos de maior interesse está relacionado à interação entre sistemas determinísticos e sistemas randômicos. Tradicionalmente, na área de equações diferencias, nós tentamos prever exatamente o que vai acontecer no futuro (sistema determinístico). Mas, no mundo real, as coisas não são assim, pois sempre há alterações imprevisíveis (sistema randômico). Entender como essas mudanças interferem nos resultados das equações diferenciais é um grande desafio atualmente”, ressalta Mallet-Paret.
Uma das transformações que vêm gerando impacto na área está ligada ao desenvolvimento tecnológico. “Ser capaz de resolver equações diferenciais no computador de forma acurada não era possível 20 anos atrás”, diz. Para ele, com o aumento da capacidade dos computadores, abre-se um vasto leque para o desenvolvimento de novas aplicações de alta relevância empregando as equações diferenciais.
Para aqueles que pensavam que tudo já estava resolvido quando o papo era matemática, vale dizer que, por estar presente em tudo, a matemática é tão infinita quanto a capacidade humana de criar. Como escreve o matemático Edward Frenkel no livro Amor e matemática: O coração da realidade escondida: “Eis como é em matemática: cada novo resultado remove o véu que cobre o desconhecido, mas o que então se torna conhecido não contém simplesmente respostas – inclui perguntas que não sabíamos formular, direções que não sabíamos que podíamos explorar. E, assim, cada descoberta nos inspira a dar novos passos e nunca nos deixa satisfeitos em nossa busca por conhecimento”.